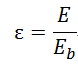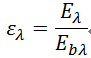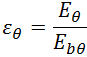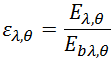热辐射的基本定律

一、普朗克定律

1900年，普朗克（M.Planck）从量子理论出发，揭示了黑体光谱辐射力和波长λ、热力学温度T之间的函数关系，它可表达为：

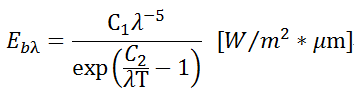
式中     λ——波长，μm；

               T——热力学温度，K；

               C₁——普朗克第一常数，；

             C₂——普朗克第二常数，

普朗克定律的黑体光谱分布如图所示。

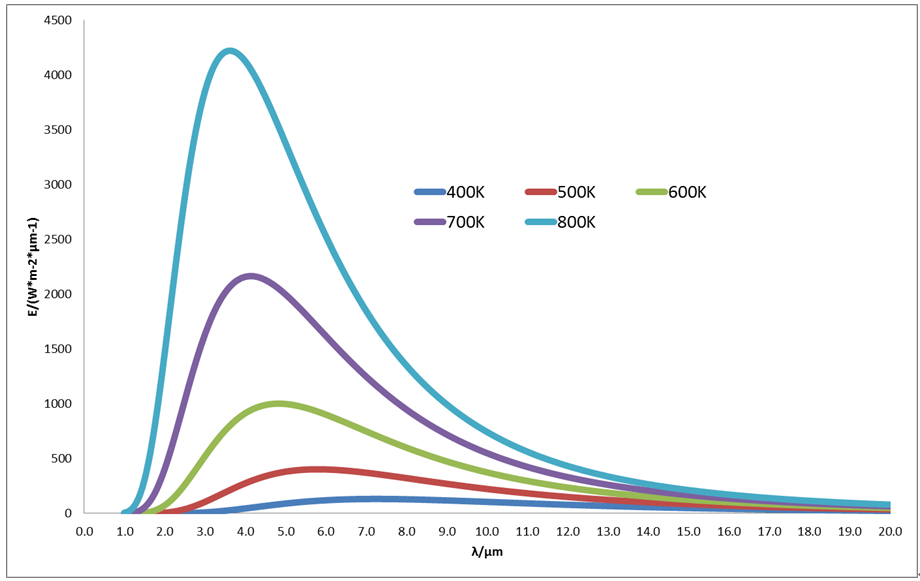
从光谱分布图可知：

1、每条曲线代表同一温度下的黑体光谱辐射力随波长的变化关系，在波长趋近于0或无穷大时，黑体光谱辐射力取决于0。

2、在某个波长上，黑体光谱辐射力会达到一个峰值，记为对应的波长称为峰值波长。

3、曲线与横坐标围成的面积表示黑体辐射力。温度升高，黑体辐射力和黑体光谱辐射力均迅速增大，且峰值波长向短波方向移动。

对普朗克定律中的黑体光谱辐射力对波长求极值，可推导出维恩位移定律：

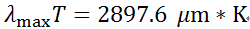
维恩位移定律说明，随着温度T的增加，最大光谱辐射力所对应的峰值波长逐渐向短波方向移动。

二、斯蒂芬——玻尔兹曼定律

斯蒂芬——玻尔兹曼定律也成为四次方定律，它说明黑体的辐射力和热力学温度的四次方成正比。表达式为：

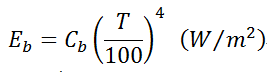
式中     ，称为黑体辐射系数。

由该定律可知，如果黑体的热力学温度增加1倍，则黑体辐射力将增加16倍。可见，随着温度的升高，辐射换热将成为热交换的主要方式。

三、基尔霍夫定律

实际物体的发射不同于黑体。它的光谱辐射力随波长和温度的变化是不规则的，不遵守普朗克定律。我们把实际物体的辐射力与相同温度黑体的辐射力之比称为该物体的发射率ε。

根据辐射力的几种定义，有几种不同的发射率。

实际物体发射率与其光谱发射率之间的关系可以用下式表示

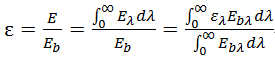
假如某物体的光谱发生率不随波长发生变化，即，则这种物体称为灰体。灰体也是一种理想化的物体。

灰体的光谱辐射力与同温度黑体光谱辐射力随波长的变化曲线完全相似。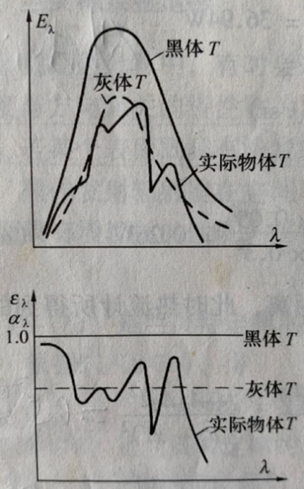

工程实践中，参与辐射换热的物体温度大多低于2000K，此时实际物体在红外波段范围内可近似地视为灰体，

这种简化处理给辐射换热计算带来很大方便。

1859年基尔霍夫（Kirchhoff）用热力学方法揭示了物体发射辐射能的能力与它吸收投射辐射能能力之间的关系，

即基尔霍夫定律，其最基本表达式为

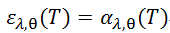
基尔霍夫定律表明，在热平衡条件下，物体表面光谱定向发射率等于该表面对同温度黑体辐射的光谱定向吸收比。

如果是漫射灰表面，则发射率与方向、波长无关，因此，漫—灰表面的发射率等于该表面的吸收比，即

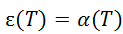
  在工程辐射换热计算中，只要参与辐射换热的各物体温差不过分悬殊，可以把物体表面当作漫射灰表面应用上述公式不会造成太大误差。